Dynamic simulation as decision support tool
So far we have mentioned how simulation presents itself as an alternative tool to the traditional problem solving methods used by decision makers within the various SCM processes.
Let us now go into the detail of this application to evaluate the main aspects inherent to the application of this methodology in the SCM context: how is a simulation model developed? What is needed for its operation? How is it actually used?
In the next paragraphs we will answer these and other questions, trying to provide a complete discussion of all the aspects inherent to the implementation of a dynamic simulation model for the governance of decisions made within SCM processes.
Which type of simulation?
When talking about simulation, we are considering a vast range of methodologies and applications that are used in very different fields. For example, FEM analysis (Finite Elements analysis), which is often carried out during the design and prototyping of a new product to test its mechanical properties in advance, represents a particular use of simulation.
In cases of application of simulation to the supply chain, we can summarize three different approaches existing in the literature:
To select the correct simulation method, a first critical decisional level is the level of abstraction of the methods. In facts, each method serves a specific range of abstraction levels, and a modeler should be deciding upon which method to use based on the problem’s characteristics.
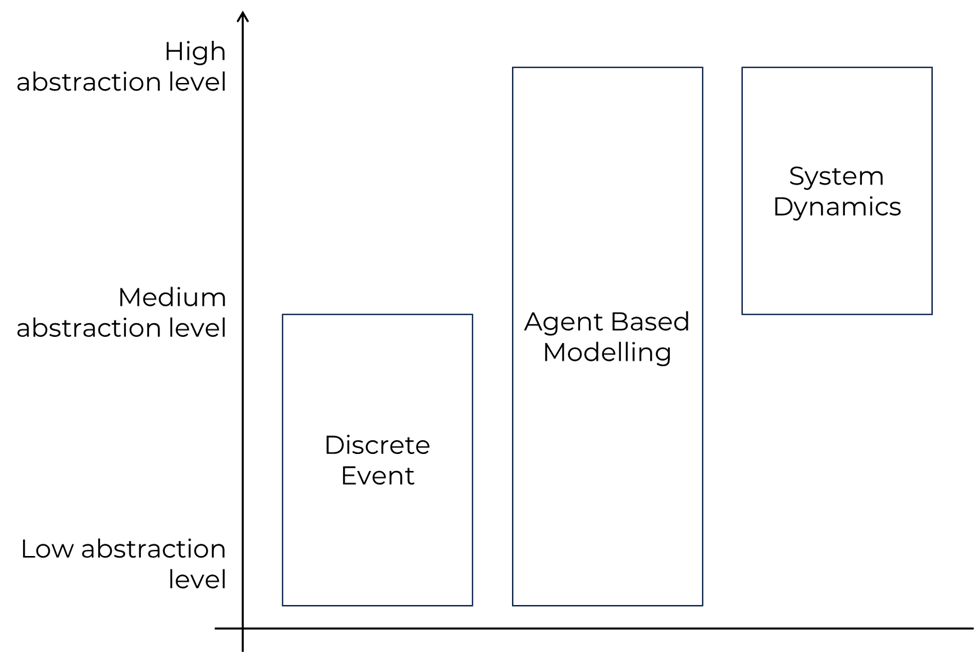
System Dynamics (SD):
System Dynamics operates at a high level of abstraction, focusing on the overall structure and behavior of a system. It represents key variables and their interconnections using causal loop diagrams (CLDs) and Stock and Flows Diagrams (SFDs), emphasizing feedback loops and accumulations. SD provides a holistic view of system dynamics but may simplify individual components, behavior, and intricate interactions.
In facts, the system behavior is defined by simple parameters interactions and mathematical relationships of parameters. For example, in an SD environmental model, the model can estimate the resource cost over time (e.g. oil) based on a mathematical the interaction of other parameters (e.g. oil extraction rate, oil consumption), but does not allow to detail the consumption in the whole world (e.g. considering tariffs) nor define different consumer behaviors (e.g. drivers in the US tend to make more miles by car than people in the Netherlands). Agent Based Modelling can overcome the SD limitations.
Agent-Based Modeling (ABM):
Agent-Based Modeling allows for a more granular level of abstraction by simulating individual agents with unique characteristics and behaviors. ABM captures the heterogeneity and autonomy of entities within a system, offering a detailed perspective on how individual components interact. This method provides a nuanced understanding of emergent patterns and behaviors, making it suitable for studying complex systems with diverse actors. Bringing back the example from SD, in this case a modeler would be able to define oil consumers from the US and from the Netherlands. Eventually, both of them could be clustered in sub-clusters based on their wealth or location (e.g. people living in big cities run less miles). This is configurable, up to each single entity behavioral simulation. In this case, oil consumption can be estimated with more precision compared to SD, and the model can predict the future consumption based on the people elasticity to price changes.
Discrete Event Modeling (DEM):
Discrete Event Modeling focuses on specific occurrences or events within a system, providing a detailed level of abstraction. It is best used to represents processes as sequences of discrete events, capturing the timing and order of activities. DE specifically focuses on process flows, making it the best method to address Supply Chain problems, which can be broken down in many sub-processes (e.g. logistics, storage, manufacturing…). While also Discrete Events allow the creation of agents, it is important to clarify the difference between Discrete Event and ABM agents.
In DE, there are two types of agents: passive and active agents. In ABM, agents are only active due to the fact that each agent has its own defined behavior and interact with each other.
To give an example of “passive” agent in DE, we can think of a production order or a lot in a manufacturing simulation model. This agent is made of configurable parameters: size, weight, color, just to provide some, but is not characterized by a pre-defined behavior as it is inanimate. Instead, other active agents (e.g. machines and human resources) containing the process flow will define the routing of the order from the beginning to the end of their life.
The tailored approach
The first fundamental element to understand about the creation of a simulation model is that it is developed starting from scratch, without any “preset” models to rely on. This is due precisely to the need to grasp the typical nuances of the business, company and supply chain : if on the one hand there may be an agreed framework on how to develop the data useful for the decision-making process, on the other hand the modeled reality is peculiar and therefore requires ad hoc modeling.
In this sense we can say that creating a simulation model for a specific company can be compared to the construction of a house: the client will rely on an architect and provides him indications about his wishes, both in terms of expected output and constraints (economic and not),. The architect will create a project capable of accommodating all requests. This does not mean that there is an absolute best project: just as happens with a house, by relying on different designers you obtain different projects that are all valid.
The critical issue therefore lies in finding the model that correctly represents the right trade-off between precision of the result provided, reliability, scalability and onerousness of implementation and maintenance (measured in cost and time).
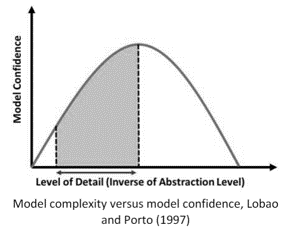
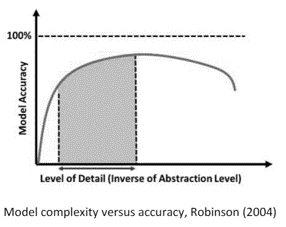
It is clear that, once the type of simulation model has been defined, the advantages of having an ad hoc model far outweigh the costs of its creation. Among them we include:
- Obtaining a local optimum solution, valid only for the analysis context. This allows to overcome the traditional limits of analytical methods: they provide global optimal solutions but with a reduction in the realism of the analyzed problem (the system must necessarily be translated into constraints), which can actually jeopardize the applicability of the solution provided.
- The possibility of “manually” managing levers, parameters and thresholds to dynamically adapt the results provided by the model to changes in the business and therefore in company objectives. This type of interaction with the model, made possible through appropriate parameter setting interfaces, allows decision makers to experiment freely and without consequences with different decision-making alternatives.
- Recurrent use of the model, to carry out ex-post or ex-ante analyses. The model also represents a useful benchmark tool for performing root-cause analysis of problems that affected the supply chain in a specific period or for verifying the causes of unexpected results.
The scalability of the model also allows the conformation of the modeled system to be modified in a short time following changes in the structure of the analyzed supply chain.
From this point of view, the addition of a warehouse, a factory or new products/components within the analyzed supply chain is much less costly, in terms of implementation times, compared to modifying/adding constraints of a analytical method (algorithm).
Mastering complexity
When we talk about complexity, it is often difficult to quantify it in a unique and easily understandable way. If on the one hand for the evaluation of traditional methods (analytical algorithms) complexity is “measurable” according to the theory of computational complexity, which analyzes the time and computational capacity required to solve a given problem, on the other hand the same methodology cannot be applied to simulation models as they “lack” a problem to solve.
Therefore, leaving aside the mathematical aspect linked to the measurement of complexity, we can limit ourselves to carrying out a qualitative analysis based on the main elements that contribute to identifying the computational complexity of a model (whether analytical or simulation).
An analytical method often considers the optimization of a precise objective variable (e.g. production cost, profit, etc.), while the simulation model limits itself to evaluating, moment by moment, the value of each variable present in the model based on its causal relationships (deterministic or stochastic) with the other variables. It follows that the choice of the objective function of an analytical method reflects the degree of specificity that you want to give to the problem through the variables used to determine the final result to be optimized. For example, in maximizing the profit of a given problem, the calculation function of that indicator could be trivially modeled as:
Profit = (price – variable cost) * quantity – fixed costs
or it may need to be furtherly sophisticated, detailing the macro variables in their primary (e.g. costs of production factors) or secondary components. The choice of the correct level of detail, linked to the “free” variables of the problem, therefore influences the system of constraints and the number of calculations (derivatives of the objective function) that must be considered.
This aspect formally constitutes an a priori choice when selecting an analytical model: the incorrect structuring of the objective function can lead to partially or completely review the system of constraints and variables considered by the problem. Furthermore, the level of detail considered in the objective function is however limited by the very nature of the algorithm: the calculation time and the goodness/applicability of the theoretical result are heavily conditioned by the number of variables and analysis dimensions included in the algorithm. This can lead some applications to propose “degenerate” solutions, that is, valid from an algorithmic point of view but difficult to implement in the reality considered.
On the contrary, a simulation model allows you to generate results based on a macro structure of links that regulate how the model variables interact with each other. This allows you to develop the first simplified “drafts” of the model and quickly test them to verify their effectiveness and the reliability of the results obtained. Based on the analysis of these results, it is then possible to proceed to define further variables to add to the model to increase the capacity and correctness of the estimate.
This development mode by addition often allows for significant time savings and satisfactory forecasting results, effectively enabling agile model development.
The number of variables in play is clearly the factor with the main impact on the complexity of the problem. Often this aspect is not known a priori, as the variables emerge gradually as the problem is analyzed and modelled.
From this point of view, the variables considered by an analytical method can be the same as those of a simulation model and vice versa. The difference between the two approaches in this case mainly concerns the clarification of how these variables interact: in the simulation model a reasoning perspective for classes of variables can be adopted while in the analytical method it is necessary to define and verify new constraints for each type of added variable.
A second aspect that has a strong impact on the complexity of the analyzed problem concerns the so-called analysis dimensions. By dimensions or classes we mean the number of sets of values that represent the different types of variables considered. Typical classes that we can find in any model (analytical and simulation) inherent to the supply chain are: products, nodes, resources, paths, time, etc. In other words, classes represent the different indexes that we can find within the objective function and constraints of an analytical algorithm.
From this point of view, the complexity of the problem grows as the classes considered increase, and there is no difference at this level between the methods.
However, although usually the number of dimensions considered for solving a problem is equivalent, the simulation differs heavily from the analytical method due to the possibility of considering time as a continuous and not discrete dimension of analysis. While each class is usually characterized by a finite (discrete) set of elements, time is an exception as it is a continuous dimension: the possibility of considering it in these terms entails various benefits for the decision maker, who not only obtains a result but is able to verify the evolution of a variable over time and analyze the main events that have modified it.
Obviously this peculiarity can also be partially captured in an analytical model by carrying out the so-called bucketization of time (division of the time horizon into equal instants) with a very small level of detail (e.g. seconds). However, this action strongly affects resolution times and is not easily usable in practice.
The complexity of a system is measurable by identifying its constituent variables, as previously described, and defining their behavior. Often the behavior of the variables representing the observed phenomena is hypothesized for convenience and simplicity of resolution, effectively compromising the goodness and adaptability of the solution to the context studied.
To give an example, often the demand recorded at a supply chain node at a certain moment is seen as an average value and is assumed to be constant over the period considered. This may prove to be an acceptable simplification for certain situations but in other cases it does not allow us to grasp any critical issues inherent to the proposed solution. Hypothesizing the probability distribution of any event already constitutes a simplification of the nature of the problem studied. Through simulation it is possible to consider continuous stochastic variables capable of approximating the analyzed reality as faithfully as possible. The importance of developing reasoning and solutions on a stochastic basis is fundamental, as:
- It allows you to analyze the results by case study (e.g. best case, worst case, most probable case), broadening the vision of decision makers and the range of actions that can be implemented (think for example of different risk management plans). This is made possible thanks to the possibility of repeating the simulation a large number of times, always generating different results from which conclusions can then be deduced according to statistical inference processes.
- It allows you to associate certain results and factors with probabilities of occurrence, which help to analyze the problem and highlight particular critical issues that must be specifically addressed.
- It allows prioritizing management efforts and resources according to a quantitative criterion.
- It allows you to link variables controllable by the decision maker (endogenous) with variables exogenous to the system, defining its degree of action on the final result.
- It teaches us to accept deviations in results from targets as part of reality and not as a result of a lack of effectiveness or efficiency in the work performed.
The optimality of a solution indicates its property of being better than other solutions according to a given criterion. It follows that optimality is a characteristic that can be attributed to a solution based on a series of criteria defined by the decision maker.
As already mentioned, simulation is not used to determine optimal solutions but rather results intended as a consequence of the behavior of the variables considered. In practice, however, it may happen that some parts of the simulation model are subject to optimization: it is in fact possible to execute particular optimization algorithms capable of to select the best result for a given parameter of the problem, under the appropriate conditions. In these applications, rather than the optimal solution per se, the decision maker is often interested in evaluating the change in the optimal solution as the model conditions vary.
Consider, for example, the determination of safety stocks within a logistics network. Theory teaches us that the calculation of the amount of such stocks at a given instant can be obtained by deriving a cost function which takes into account a series of costs linked to the management of stocks and the failure to provide a service (relating to the lack of stock ). This allows you to identify a unique value, given a series of values set for the input variables (such as demand or desired service level).
In a similar application, but developed with a simulation model, the decision maker has at his disposal a series of levers on which he can act (e.g. service level, storage capacity, financial immobilization) and a series of exogenous variables on which he cannot act (e.g. variability in demand). He will therefore be able to simulate different plausible scenarios to check what happens to different indicators, varying from time to time the sets of values that can be used to define the available levers .
A factor that can be objectively measured is the precision of the estimate made by the model. In this case, as happens with many statistical models (e.g. regressive, correlative, etc.), precision can be measured by the deviation recorded between the expected result (obtained through the model) and the actual result. In statistics, the sum of the squares of these deviations (MSE method) therefore constitutes the term to be optimized (minimized) to refine the model’s estimation capacity by acting on its parameters. In simulation, however, this procedure is not easily implementable because there are often many links between different “intermediate” variables that contribute to determining the result of the “final” variables (results of the simulation model). These intermediate variables cannot be directly verified as the final data to make a comparison is often missing.
Let’s take the example of safety stocks in a logistics network again: let’s say that the simulation model allows an estimate of the service level, based on a history of orders, of 85% while in reality a service level was measured by 90%. It is clear that the result of the model can be traced back to a series of different factors, such as: network reactivity (order processing time), transportation times, initial stock level, stock management policies, etc. These variables, which are placed in an “intermediate” layer between the primary variable of the demand and between the result of the model relating to the service, are often difficult to verify with final data. So how can the simulation model guarantee the accuracy of its results? In the face of deviations, the model allows us to trace the various component variables of the result and verify their status (i.e. the value assumed at each instant of time) to highlight anomalous situations capable of explaining the divergence of the result obtained compared to the expected according to a cause-effect logic. By doing so it is possible to correct the simulation model in progress, until obtaining a tool capable of faithfully replicating reality. If at the end of the corrections, which are often necessary to capture specific aspects of the company’s business, the model still presents significant variances in its results, it is a good idea to check under which hypotheses and reasoning the final results were calculated. In fact, it is not uncommon that in reality we often tend to make calculations and simplifications on the starting data (e.g. to remove a series of orders when calculating the service level for a specific reason), thus obtaining results that may differ from the ones of the model which however are more realistic in practice.
01
Problem solving in supply chain processes
Problem by problem: Analytical methods and Dynamic Simulation compared
02
Dynamic simulation as decision support
How to choose the right simulation methodology for a tailor made approach to reliable data-driven decision
04
Skills and technologies
Learn about the skills and technologies involved in this cutting-edge technology
06
Applying Simulation to the S&OP process
MRP, Scheduling, and in between Simulation Modelling: discover how